本文分两部分,第一部分列举几个有趣的位操作,
第二部分讲解算法中常用的 n & (n – 1) 操作,
顺便把用到这个技巧的算法题列出来讲解一下。
因为位操作很简单,所以假设读者已经了解与、或、异或这三种基本操作。
一、几个有趣的位操作
-
利用 或操作
|和空格 将英文字符转换为小写
(‘a’ | ‘ ‘) = ‘a’
(‘A’ | ‘ ‘) = ‘a’
-
利用 与操作
&和下划线 将英文字符转换为大写
(‘b’ & ‘_’) = ‘B’
(‘B’ & ‘_’) = ‘B’
-
利用 异或操作
^和空格 进行英文字符大小写互换
(‘d’ ^ ‘ ‘) = ‘D’
(‘D’ ^ ‘ ‘) = ‘d’
PS:以上操作能够产生奇特效果的原因在于 ASCII 编码。
字符其实就是数字,恰巧这些字符对应的数字通过位运算就能得到正确的结果,
-
判断两个数 是否异号
int x = –1, y = 2;
bool f = ((x ^ y) < 0); // true
int x = 3, y = 2;
bool f = ((x ^ y) < 0); // false
PS:这个技巧还是很实用的,利用的是补码编码的符号位。
如果不用位运算来判断是否异号,需要使用 if else 分支,还挺麻烦的。
读者可能想利用乘积或者商来判断两个数是否异号,
但是这种处理方式可能造成溢出,从而出现错误。
-
交换两个数
int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;
// 现在 a = 2, b = 1
-
加一
int n = 1;
n = –~n;
// 现在 n = 2
-
减一
int n = 2;
n = ~–n;
// 现在 n = 1
PS:上面这三个操作就纯属装逼用的,没啥实际用处,大家了解了解乐呵一下就行。
二、算法常用操作 n&(n-1)
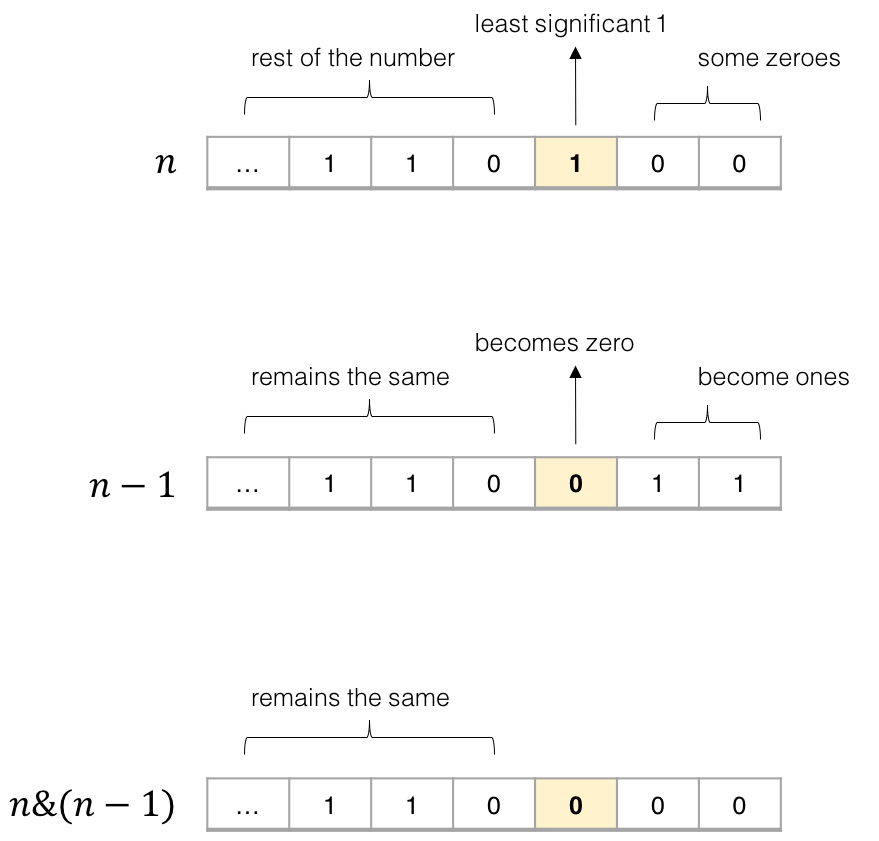
这个操作是算法中常见的,作用是:
消除数字 n 的二进制表示中的最后一个 1。
看个图就很容易理解了:
-
计算汉明权重(Hamming Weight)

就是让你返回 n 的二进制表示中有几个 1。
因为 n & (n – 1) 可以消除最后一个 1,
所以可以用一个循环不停地消除 1 同时计数,直到 n 变成 0 为止。

-
判断一个数是不是 2 的指数
一个数如果是 2 的指数,那么它的二进制表示一定只含有一个 1:
2^0 = 1 = 0b0001
2^1 = 2 = 0b0010
2^2 = 4 = 0b0100
如果使用位运算技巧就很简单了(注意运算符优先级,括号不可以省略):


