本文就解决一类最难掌握的双指针技巧：滑动窗口技巧。
这个算法技巧的思路非常简单，就是维护一个窗口，不断滑动，然后更新答案。
LeetCode 上有起码 10 道运用滑动窗口算法的题目，难度都是中等和困难。
该算法的大致逻辑如下：
int left = 0, right = 0;
while (right < s.size()) {`
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}
这个算法技巧的时间复杂度是 O(N)，比字符串暴力算法要高效得多。
其实困扰大家的，不是算法的思路，而是各种细节问题。比如说如何向窗口中添加新元素，如何缩小窗口，在窗口滑动的哪个阶段更新结果。
所以今天我就写一套滑动窗口算法的代码框架，以后遇到相关的问题，你就默写出来如下框架然后改三个地方就行，还不会出 bug：
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
其中两处 ... 表示的更新窗口数据的地方，到时候你直接往里面填就行了。
而且，这两个 ... 处的操作分别是右移和左移窗口更新操作，等会你会发现它们操作是完全对称的。
言归正传，下面就直接上四道 LeetCode 原题来套这个框架，其中第一道题会详细说明其原理，后面四道就直接闭眼睛秒杀了。
本文代码为 C++ 实现，不会用到什么编程方面的奇技淫巧，但是还是简单介绍一下一些用到的数据结构，以免有的读者因为语言的细节问题阻碍对算法思想的理解：
unordered_map 就是哈希表（字典），它的一个方法 count(key) 相当于 Java 的 containsKey(key) 可以判断键 key 是否存在。
可以使用方括号访问键对应的值 map[key]。需要注意的是，如果该 key 不存在，C++ 会自动创建这个 key，并把 map[key] 赋值为 0。
所以代码中多次出现的 map[key]++ 相当于 Java 的 map.put(key, map.getOrDefault(key, 0) + 1)。
一、最小覆盖子串
LeetCode 76 题，Minimum Window Substring，难度 Hard：
就是说要在 S(source) 中找到包含 T(target) 中全部字母的一个子串，且这个子串一定是所有可能子串中最短的。
滑动窗口算法的思路是这样：
1、我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为一个「窗口」。
2、我们先不断地增加 right 指针扩大窗口 [left, right)，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。
3、此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right)，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。
4、重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。
这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解，也就是最短的覆盖子串。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动，这就是「滑动窗口」这个名字的来历。
下面画图理解一下，needs 和 window 相当于计数器，分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。
初始状态：
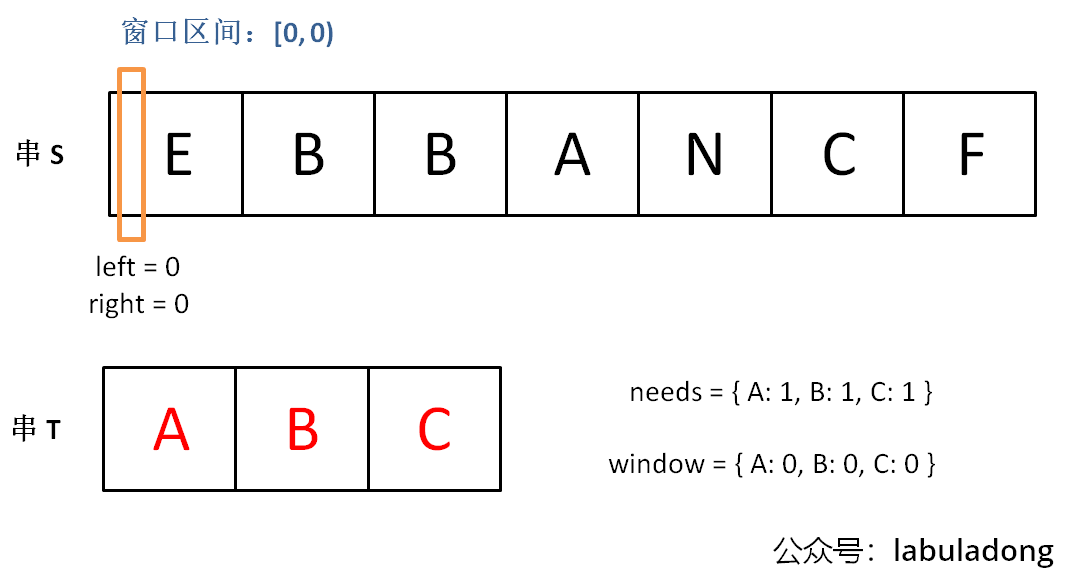
增加 right，直到窗口 [left, right] 包含了 T 中所有字符：
现在开始增加 left，缩小窗口 [left, right]。
直到窗口中的字符串不再符合要求，left 不再继续移动。
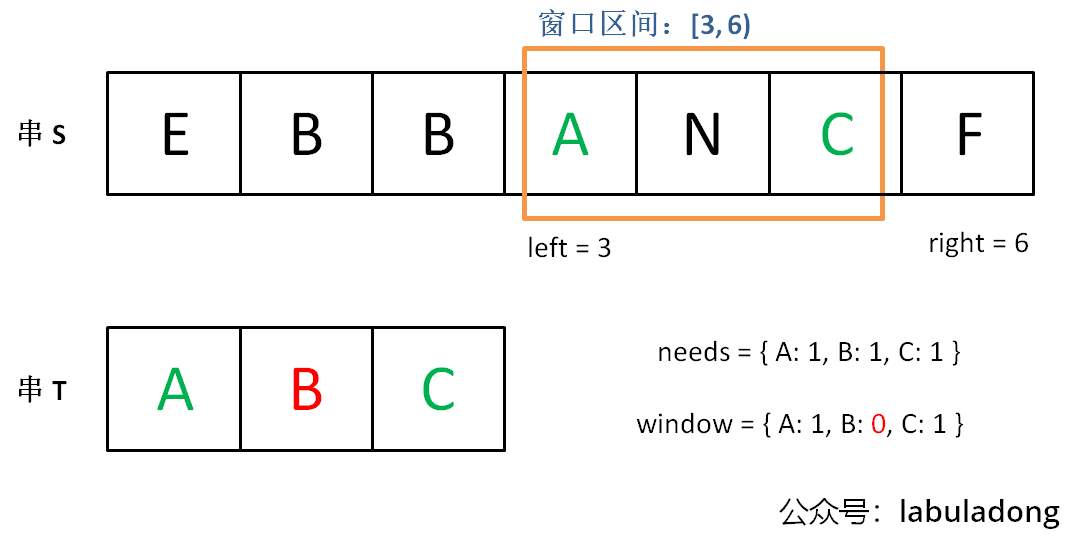
之后重复上述过程，先移动 right，再移动 left…… 直到 right 指针到达字符串 S 的末端，算法结束。
如果你能够理解上述过程，恭喜，你已经完全掌握了滑动窗口算法思想。现在我们来看看这个滑动窗口代码框架怎么用：
首先，初始化 window 和 need 两个哈希表，记录窗口中的字符和需要凑齐的字符：
然后，使用 left 和 right 变量初始化窗口的两端，不要忘了，区间 [left, right) 是左闭右开的，所以初始情况下窗口没有包含任何元素：
其中 valid 变量表示窗口中满足 need 条件的字符个数，如果 valid 和 need.size 的大小相同，则说明窗口已满足条件，已经完全覆盖了串 T。
现在开始套模板，只需要思考以下四个问题：
1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？
2、什么条件下，窗口应该暂停扩大，开始移动 left 缩小窗口？
3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？
4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？
如果一个字符进入窗口，应该增加 window 计数器；如果一个字符将移出窗口的时候，应该减少 window 计数器；当 valid 满足 need 时应该收缩窗口；应该在收缩窗口的时候更新最终结果。
下面是完整代码：
string minWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = INT_MAX;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (valid == need.size()) {
// 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
// 返回最小覆盖子串
return len == INT_MAX ?
"" : s.substr(start, len);
}
需要注意的是，当我们发现某个字符在 window 的数量满足了 need 的需要，就要更新 valid，表示有一个字符已经满足要求。而且，你能发现，两次对窗口内数据的更新操作是完全对称的。
当 valid == need.size() 时，说明 T 中所有字符已经被覆盖，已经得到一个可行的覆盖子串，现在应该开始收缩窗口了，以便得到「最小覆盖子串」。
移动 left 收缩窗口时，窗口内的字符都是可行解，所以应该在收缩窗口的阶段进行最小覆盖子串的更新，以便从可行解中找到长度最短的最终结果。
至此，应该可以完全理解这套框架了，滑动窗口算法又不难，就是细节问题让人烦得很。以后遇到滑动窗口算法，你就按照这框架写代码，保准没有 bug，还省事儿。
下面就直接利用这套框架秒杀几道题吧，你基本上一眼就能看出思路了。